Principes

Sous-programmes récursifs

Un sous-programme est récursif si il s'appelle lui même, c'est à dire que le corps de ce sous-programme contient une instruction d'appel de ce même sous-programme.

Exemple de sous-programme récursif (langage Java):

int Factorielle (int n)
{
   if (n == 1) {
     return 1;
   }
   else return n * Factorielle(n - 1);
}

De manière plus générale, on dira qu'un sous-programme est récursif s'il s'appelle de manière directe (comme dans l'exemple précédent) ou de manière indirecte. Par exemple si un sous-programme A contient un appel à un sous-programme B, qui lui même contient un appel du sous-programme A, on pourra toujours considérer que le sous-programme A est récursif bien qu'il ne contient aucun appel de lui même.

Résoudre un problème par récursivité

Pour résoudre un problème de manière récursive (c'est à dire en utilisant des sous-programme récursifs), il faut commencer par se poser la question suivante:

Si la réponse est oui, il est possible d'envisager une solution récursive.

Il est assez difficile de définir ce que signifie "la taille" d'un problème de manière générale. Très souvent, il s'agit d'un entier n définissant la dimension des données à traiter. Par exemple, si la donnée du problème est une liste, ce sera le nombre d'éléments de cette liste. On se demandera alors s'il est possible de résoudre le problème sur une liste de longueur n à partir de la solution du même problème sur une liste de longueur n-1.

Il est également indispensable que le problème ait une solution évidente lorsque n est très petit (0 ou 1 typiquement).

Exemple1 : la factorielle

Prenons par exemple le problème du calcul de la factorielle d'un nombre entier. Par définition, la factorielle d'un nombre entier n ≥ 1, noté n! est le calcul:
n! = n × (n-1) × ... × 2 × 1.

On voit donc que le calcul de (n-1)! est contenu dans celui de n!. En supposant que l'on sache calculer (n-1)!, il suffira de multiplier le résultat de ce calcul par n, pour obtenir n!.

Cette simple constatation donne la solution du problème sous la forme d'une fonction récursive:

int Factorielle (int n)
{
   if (n == 1) {
     return 1;
   }
   else return n * Factorielle(n - 1);
}

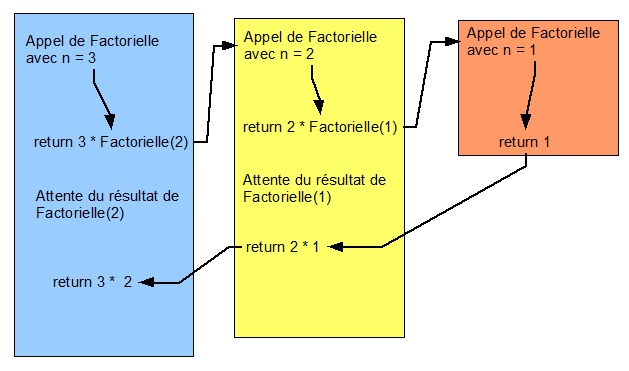
Déroulement du programme pour n = 3

Exemple2 : les tours de Hanoi

Présentation du problème

Le problème des tours de Hanoi est un casse tête que l'on utilise souvent pour montrer l'intérêt de la récursivité. Contrairement à l'exemple précédent (la factorielle), il n'est pas facile de trouver une solution purement itérative (avec des boucles) à ce problème.

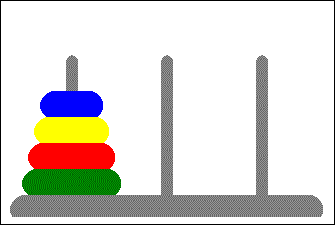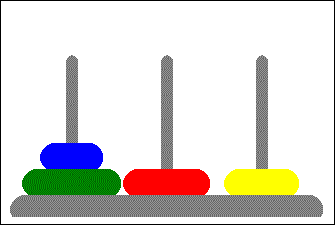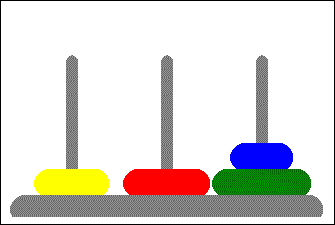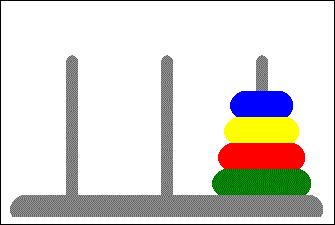
Le casse tête est composé de trois tiges verticales sur lesquelles on peut enfiler des disques troués de différents diamètres:

Au début, tous les disques sont enfilés sur une des tiges dans l'ordre décroissant (le plus grand en bas). Il s'agit de déplacer toute la pile sur une autre tige en respectant les deux règles suivantes :

• Il est interdit de déplacer plusieurs disques en même temps.
• Il est interdit de placer un disque sur un disque plus petit que lui.

Voici par exemple une solution pour une tour de quatre disques:

Formulation récursive du problème

Est-il possible de résoudre le problème de Hanoi avec n disques à partir d'une solution pour n-1 disques ?

Ce n'est pas évident à première vue, mais effectivement, une formulation récursive de ce problème est possible. Prenons le cas d'une tour à trois disques:

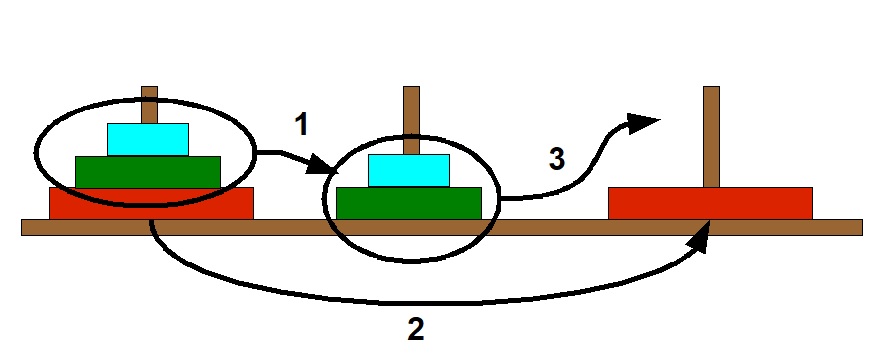
En supposant que l'on sache résoudre le problème pour une tour à deux disques, on peut résoudre le problème pour une tour à trois disques en trois étapes:

1. Déplacer la pile composée des deux disques supérieurs de la tour de départ à la tour intermédiaire.
2. Déplacer le plus grand disque de la tour de départ vers la tour d'arrivée.
3. Déplacer la pile composée des deux disques supérieurs de la tour intermédiaire à la tour d'arrivée.

On peut évidemment généraliser ce principe à une tour composée de n disques. En supposant que l'on sache résoudre le problème pour une tour à n-1 disques, on peut résoudre le problème pour une tour à n disques en trois étapes:

1. Déplacer la pile composée des n-1 disques supérieurs de la tour de départ à la tour intermédiaire.
2. Déplacer le plus grand disque de la tour de départ vers la tour d'arrivée.
3. Déplacer la pile composée des n-1 disques supérieurs de la tour intermédiaire à la tour d'arrivée.

Implémentation récursive en php

Le plus dur est fait: nous avons la formulation récursive du problème. Il ne reste plus qu'à traduire cela en un sous-programme récursif. Voilà, par exemple la traduction en Php:

   function Hanoi($n,$D,$A,$I) {
     if ($n != 0) {
       Hanoi($n-1,$D,$I,$A);
       Deplacer ($D, $A);
       Hanoi($n-1,$I,$A,$D);
     }   
   }

Dans cette procédure $n désigne le nombre de disques, $D est le numéro de la tour de départ, $A est le numéro de la tour d'arrivée est $I, celui de la tour intermédiaire. La procédure Deplacer déplace un disque de la tour numéro $D à la tour numéro $A.

Déroulement du programme pour n=3

Exécuter le programme pour n=3..

Trace des appels récursifs pour n=3..