Utilisation des procédures

Exemple1

Concevoir un programme à l'aide de sous-programmes signifie découper un traitement en sous-traitements spécifiques. Pour illustrer ceci, reprenons le projet Peinture du cours Première Notion.

Peinture.jpg, 21kB

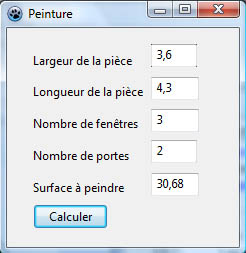
Rappelons que ce programme permet de calculer la surface à peindre d'une pièce rectangulaire connaissant les dimensions de la pièce (longueur, largeur), le nombre de fenêtres et le nombres de portes.

Cet exemple nous avait justement servi à illustrer le principe du découpage d'un traitement en sous-traitements. Lorsqu'un calcul est trop complexe, on a intérêt à le découper en plusieurs calculs intermédiaires et sauvegarder les résultats intermédiaires dans des variables.

Cela nous avait donné le code suivant pour le bouton Calculer.

Nous avons ici un exemple de code qui peut très facilement se réécrire à l'aide de sous-programmes. Associons un appel de procédure à chaque traitement. Cela nous donne:

PeintureAppelProc.jpg, 67kB

Comparez ce code à celui de la version précédente: il est devenu plus court et plus lisible.

Ecrivons à présent le code des procédures de calcul. Ce code doit être écrit avant la procédure évènementiel BT_CalculClick. Il suffit d'écrire une entête pour chaque procédure, puis de copier en-dessous l'affectation correspondante enrobée de begin end. On obtient ceci.

Programmation descendante

Remarquez que l'on aurait put procéder ainsi dès le départ: notre problème est de calculer la surface à peindre. Ce problème peut être décomposer en quatre sous-problèmes: calculer la surface des murs, la surface des fenêtres, la surface des portes et finalement la surface à peindre.

On associe à chaque problème une procédure, ce qui nous permet d'écrire le code du programme sans nous occuper des détails, c'est à dire avant même d'avoir résolu les sous-problèmes.

ProgDescendante.jpg, 45kB

Cette manière de procéder est la programmation descendante.

Retour d'un sous-programme

Lorsqu'une procédure évènementielle a fini de s'exécuter, le programme retourne automatiquement à un état d'attente d'évènement.

Dans le cas d'un sous-programme non évènementiel c'est un peu différent: l'ordinateur revient à l'instruction qui suit l'appel. Dans le cas du projet Peinture, on obtient ceci.