Exemple

---

Exemple 1: Organisation des fichiers

L'organisation des fichiers sur un support de stockage (disque dur, clé USB, etc...) est une organisation arborescente.

Le support contient des fichiers et des dossiers. Les dossiers peuvent contenir à leur tour des dossiers et des fichiers.

Exemple:

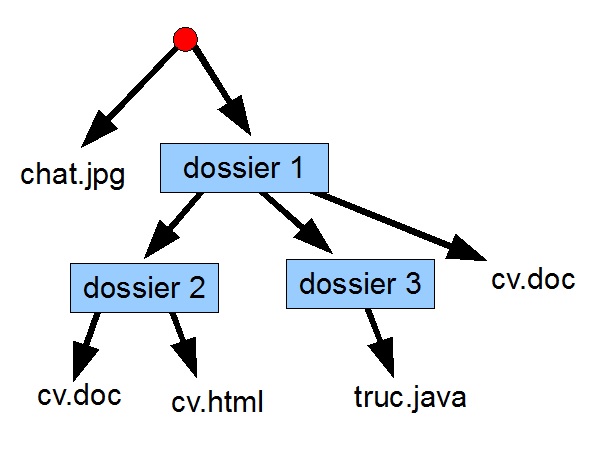
Le support de stockage (représenté par un rond rouge dans la figure ci-dessus) ainsi que les dossiers et les fichiers qu'il contient sont les noeuds de l'arbre.

Certains noeuds possèdent des noeuds fils. Dans le cas d'une arborescence de fichier, se sont les dossiers non vides ou le support de stockage (s'il est non vide). Leurs fils, sont les dossiers ou fichiers qu'ils contiennent directement.

Dans l'exemple illustré par la figure ci-dessus, le noeud dossier1 possède trois fils: dossier2, dossier3 et le fichier cv.doc.

Lorsqu'un noeud possède un fils, il existe un arc reliant ce noeud à son fils. Les arcs sont représentés dans la figure ci-dessus par les flèches.

Les noeuds qui ne possèdent aucun fils sont les feuilles de l'arbre. Dans une arborescence de fichiers, se sont les fichiers ou les dossiers vide.

Dans l'exemple illustré par la figure ci-dessus, les feuilles de l'arbre sont les fichiers chat.jpg, cv.doc (présenté deux fois), cv.html et truc.java.

Dans un arbre, il existe toujours un unique noeud qui n'est le fils d'aucun autre noeud: c'est la racine de l'arbre. Dans une arborescence de fichiers, la racine est représentée par le support de stockage (représenté par un rond rouge dans notre figure).

Un arbre est une structure récursive, car il est lui même constitué de sous-arbres. En effet, à partir de chaque noeud n d'un arbre on peut construire un sous-arbre qui possède ce noeud particulier comme racine. Les noeuds de ce sous-arbre sont les descendants de n.

Voici par exemple, le sous-arbre de racine dossier 1, dans l'arbre de la figure précédente:

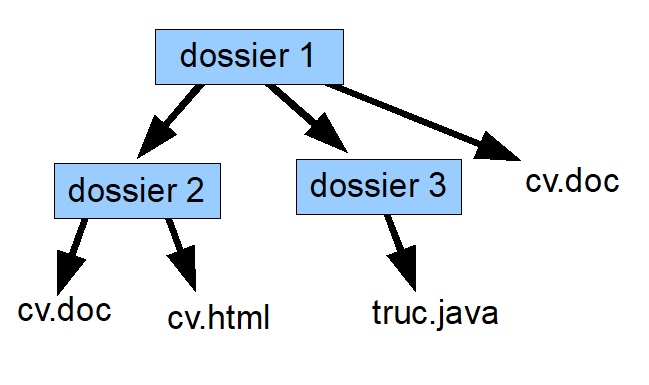
Les descendants de dossier1 sont dossier1, dossier2, dossier3, cv.doc, cv.html et truc.java.

---

Exemple 2: Classification

Une classification est un arbre dans lequel les noeuds sont les catégories. Les sous-catégories d'une catégorie sont ses noeuds fils.

Voici par exemple une classification (très sommaire) des animaux:

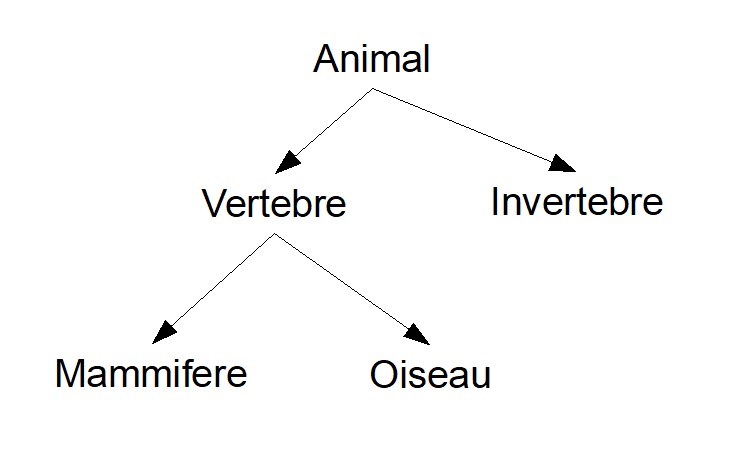
La catégorie Animal est la racine de l'arbre. Elle possède deux fils : les catégories Vertebre et Invertebre.

La catégorie Vertebre possède également deux fils: les catégories Mammifere et Oiseau.

Les feuilles de l'arbre sont les catégories Mammifere, Oiseau et Invertebre.

---

Exemple 3: Arbre de jeu

Dans les jeux à deux joueurs que nous allons voir un peu plus loin, il est utile de définir la notion d'arbre de jeu. Cet arbre représente tous les parties possibles à partir d'une situation donnée.

Voici par exemple un arbre de jeu pour le jeu du morpion.

Le morpion est un jeu qui se joue sur une grille de trois lignes et trois colonnes. Chacun des joueurs possède un symbole (croix ou rond). Le premier qui arrive à aligner trois symboles a gagné.

Les noeuds réprésentent les situations de jeu. Les situations où c'est aux croix de jouer (on dit que les croix ont le trait) sont nommées X₁,X₂,...,X₇. Celles où c'est aux rond de jouer sont nommées O₁,O₂,...,O₇.

L'arbre représenté ici appartient à une catégorie d'arbre un peu particulière appelé arbre étiqueté, car chaque arc possède une étiquette.

Dans le cas d'un arbre de jeu, chaque arc est étiqueté par le coup qu'il représente.

Remarquez que plusieurs arcs peuvent avoir la même étiquette. Cela signifie donc que l'on ne peut pas identifier un arc par son étiquette. Par contre, deux arcs partant d'un noeud donné ont forcément des étiquettes distinctes.

Dans notre exemple, il y a cinq arcs étiqueté C3. Par contre, il y en a un seul partant de la situation X₁. Si les croix jouent C3 dans cette situation, ils mettent le jeu dans la sitation O3.

Nous verrons des arbres étiquetés à deux reprise dans ce cours: dans la partie consacrée à l'exploration d'alternatives et dans celle consacrée aux jeux déterministes.

J'en profite donc pour introduire ici un peu de terminologie qui nous sera utile dans ces deux parties.

Commençons par la notion de chemin.

Dans un arbre, chaque noeud peut être atteint en partant de la racine par une unique suite d'arcs que l'on appelle son chemin.

Par exemple, le chemin de X₅ est C2-C3, le chemin de O₆ est C3-A2-C2.

Nous pouvons à présent aborder la notion de profondeur.

La profondeur d'un noeud est la longueur de son chemin. Le noeud X₅ a une profondeur 2 et O₆ a une profondeur 3. La racine a une profondeur 0.

Enfin, la profondeur d'un arbre est la longueur du plus grand chemin de cet arbre. Dans notre exemple, nous avons un arbre de profondeur 3.

Représentation par pointeurs

Un arbre peut être représenté en mémoire à l'aide de pointeurs. Pour en expliquer le principe, reprenons l'exemple de la classification des animaux. Nous allons en donner une représentation en Javascript (vous trouverez le code source de cet exemple dans le fichier Exemple-Recursivite/Classification.js).

Je précise qu'il s'agit uniquement ici de représenter des arbres non étiquetés. La représentation d'arbre étiqueté ne sera pas abordée dans ce cours.

Représentation d'un noeud

Voici un extrait de la déclaration de la classe Categorie:

 function Categorie (n,fs,fr) { 
   
   this.Nom = n;
   this.Fils = fs; 
   this.Frere = fr; 
   .
   .
   }

Le principe de représentation est basé sur les deux attributs Fils et Frere. Fils pointe vers la liste des fils (en fait, la première catégorie de cette liste) et Frere, vers le fils suivant (et Frere = null, si c'est le dernier fils de la liste)

En particulier, si le noeud est une feuille de l'arbre, son attribut Fils vaut null.

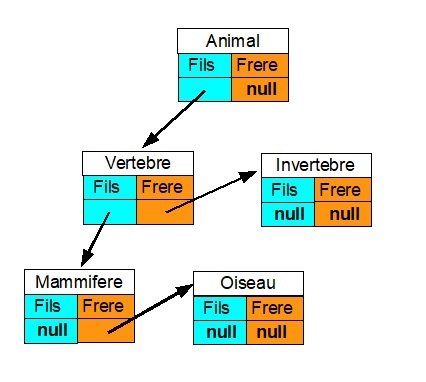
Voici par exemple la représentation sous forme de pointeurs de l'exemple d'arbre des catégories présenté précédemment (cliquer ici pour voir cet arbre dans le cadre droit):

Adjonction d'un noeud

Le petit programme que nous avons écrit permet d'ajouter de nouvelles catégories à cette classification. Vous pouvez l'exécuter dans le cadre droit en cliquant ici.

L'arbre apparait dans une zone de texte sous forme indenté. Pour ajouter la sous-catégorie Poisson à la catégorie Vertebre, on saisit ces deux noms dans les champs Catégorie et Sous-Catégorie :

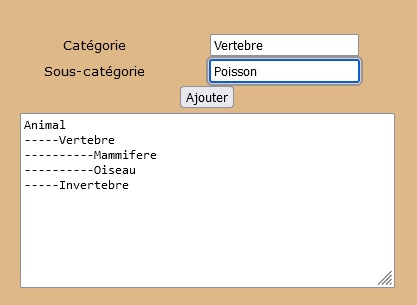
Après avoir cliqué sur le bouton Ajouter, la catégorie Poisson devient un noeud fils de la catégorie Vertebre :

Cette action est réalisée à l'aide de la méthode Ajouter_Sous_Categorie de la classe Categorie. Voici le code de cette méthode:

 this.Ajouter_Sous_Categorie = function (sc) {

       if (this.Fils==null) { this.Fils=sc;  }
       else {
         var premier_fils;
         premier_fils = this.Fils;
         this.Fils = sc;
         sc.Frere = premier_fils;
      }

Cette méthode ajoute sc dans la liste des sous-catégories de this (la catégorie à laquelle est appliquée la méthode). Il y a deux possibilités:

1. this n'a pas de fils (this.Fils == null) . Dans ce cas, il suffit de stocker l'adresse de sc dans l'attribut Fils de this.
2. Si ce n'est pas le cas, on ajoute sc au début de la liste des fils de this. Il faut faire attention à ne pas perdre l'adresse du premier fils (this.Fils). Ce pointeur est donc d'abord sauvegardé dans la variable premier_fils. Après l'affectation this.Fils=sc, la catégorie sc devient le premier fils de this. Puis on la relie à la liste des fils par sc.Frere = premier_fils.

Recherche d'un noeud

Le programme est protégé contre les erreurs de manipulation. Vous ne pouvez pas ajouter une sous-catégorie à une catégorie, si la catégorie n'existe pas ou si la sous-catégorie existe déjà (dans une classification une catégorie ne peut pas figurer à deux endroits de l'arbre). Vous pouvez faire le test en cliquant ici.

Ces erreurs sont détectées par la méthode Rechercher_Categorie(n). Appliquée à un noeud particulier de l'arbre, elle recherche une catégorie de nom n parmis ses descendants. S'il existe bien une telle catégorie, le résultat retourné est l'adresse de cette catégorie. Sinon, le résultat est null. Voici son code:

this.Rechercher_Categorie = function (n) {
    
      var resultat = null, un_fils;
    
      if (this.Nom == n) return this;
    
      if (this.Fils == null) return null;
    
      un_fils = this.Fils;
    
      while (un_fils != null) {
        resultat = un_fils.Rechercher_Categorie(n);
        if (resultat != null) return resultat;
        un_fils = un_fils.Frere;
      }
    
      return null;
                                           
    }

Plusieurs cas possibles:

1. Le nom de this est n : dans ce cas le résultat est this. Autrement dit, la catégorie recherchée est celle à laquelle on a appliqué la méthode.
2. n n'est pas le nom de this et de plus this est une feuille de l'arbre (this.Fils == null). Dans ce cas, this est son seul descendant. Comme son nom n'est pas n, le résultat est null.
3. Dans les autres cas, nous utilisons la récursivité. S'il existe un noeud nommé n parmis les descendants de this, ce noeud doit être un descendant d'un des fils de this. On applique donc simplement la méthode de recherche à tous les fils de this. Dès que le résultat est différent de null, nous avons trouvé notre catégorie !

Pointeur vers le père

Comme dans toutes les représentations basées sur des pointeurs, il peut être intéressant d'ajouter des pointeurs inverses pour faciliter certaines opérations.

Dans le cas des arbres, on peut par exemple ajouter un pointeur d'un noeud vers son pere, c'est à dire le noeud dont il est le fils. L'adresse de ce noeud pourrait être stockée dans n.Pere par exemple. Si n est la racine de l'arbre, on aura n.Pere == null.

Ce pointeur supplémentaire simplifie en particulier la suppression d'un noeud.

Nous n'entrerons pas dans les détails sur ce point. Le lecteur interessé pourra approfondir la gestion des arbres en faisant l'exercice de ce cours sur la classification (version plus élaborée que le programme de classification vu ici).