Preuve de la décidabilité (cas particulier)

Avant d'aborder la démonstration générale (n'importe quel jeu, n'importe quelle situation), voyons tout d'abord un cas très particulier (probablement qu'après avoir lu ce qui suit, vous serez convaincu que la propriété est vraie dans le cas général).

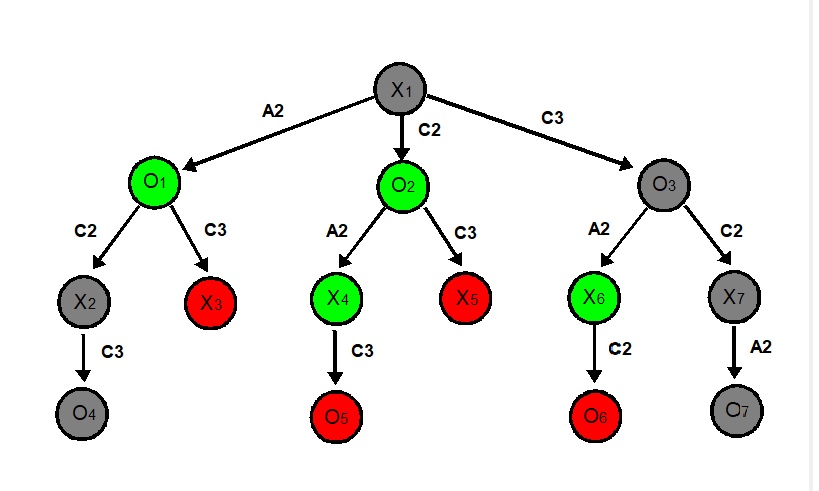
Nous allons prendre la situation suivante au jeu du morpion:

Dans cette situation de jeu nommée X₁, les croix ont le trait. Nous allons montrer qu'elle est décidable.

La preuve est basée sur l'arbre de jeu développé à partir de cette situation. Le voici.

Cet arbre visualise toutes les continuations possibles du jeu à partir de la situation X₁.

Notez que les noeuds de profondeur paire (X₁,X₂,...,X₇) représentent des situations où les croix ont le trait et inversement, les noeuds de profondeur impaire (O₁,O₂,...,O₇) représentent des situations où les ronds ont le trait.

Les feuilles représentent des situations de fin de jeu. Plus précisément:

• Pour O₄ et O₇ : partie nulle.
• Pour O₅ et O₆: les croix ont gagnés.
• Pour X₃ et X₅: les ronds ont gagnés.

Ces situations terminales sont évidemment décidables. Nous allons voir que l'on peut en déduire progressivement la décidabilité de tous les autres noeuds de l'arbre jusqu'à celle de la racine.

Le raisonnement est en quelque sorte "récursif".

Décidabilité de X₁

Partons de la racine X₁. Elle possède trois fils (O₁,O₂ et O₃).

Je prétend que si ces trois situations sont décidables, alors X₁ l'est aussi nécessairement.

En effet, il y a deux possibilités:

1. Au moins une de ces trois situations est perdante pour les ronds. Dans ce cas, les croix choisirons le coup menant à cette situation ( je l'appelerais coup gagnant par la suite) et par conséquent, ils sont certains de gagner. X₁ serait donc gagnante pour les croix.
2. Aucune de ces trois situations n'est perdante pour les ronds. Elles mènent donc toutes à une victoire des ronds ou à partie nulle. Dans ce cas, il y a également deux possibilités:
   1. Au moins une des trois situations mène à une partie partie nulle. Dans ce cas, les croix choisirons le coup menant à cette situation, car les autres mènent à une victoire certaine des ronds. Comme les croix peuvent choisir ce coup, X₁ serait donc une situation menant à une partie nulle.
   2. Toutes les trois situations mènent à une victoire des ronds. Dans ce cas, les croix perdent quelque soit le coup choisit. X₁ serait donc une situation menant à une défaite des croix.

A présent, il nous suffit de montrer que O₁,O₂ et O₃ sont décidables. Commencons par O₁.

Décidabilité de O₁

O₁ possède deux fils X₂ et X₃, or ces deux situations sont décidables. En effet:

• A partir de X₂, il n'y a qu'un seul coup possible pour les croix (C₃) et il mène à une partie nulle. X₂ conduit donc forcément à une partie nulle.
• X₃ est une situation terminale gagnante pour les ronds. Ils peuvent obtenir cette situation en jouant C₃.

A partir de O₁, les ronds ont donc un coup gagnant. En conclusion, cette situation mène obligatoirement à une victoire des ronds.

Décidabilité de O₂

O₂ possède deux fils X₄ et X₅. Montrons qu'ils sont tous les deux décidables:

• A partir de X₄, il n'y a qu'un seul coup possible pour les croix (C₃). Ce coup les mène à la victoire. X₄ conduit donc forcément à la victoire des croix. Cela signifie que les ronds ne doivent pas jouer A₂.
• X₅ est une situation terminale gagnante pour les ronds. Ils peuvent obtenir cette situation en jouant C₃.

Les ronds ont encore une fois un coup gagnant (C₃) et par conséquent O₂ est une situation qui mène forcément à la victoire des ronds.

Décidabilité de O₃

O₃ possède deux fils X₆ et X₇. Montrons qu'ils sont tous les deux décidables:

• A partir de X₆, il n'y a qu'un seul coup possible pour les croix (C₂). Ce coup les mène à la victoire. X₆ conduit donc forcément à la victoire des croix. Cela signifie que les ronds ne doivent pas jouer A₂.
• A partir de X₇, il n'y a qu'un seul coup possible pour les croix (A₂). Ce coup les mène à une partie nulle. X₆ conduit donc forcément à une partie nulle.

Ici les ronds n'ont pas de coup gagnant, mais en jouant C₂ il peuvent assurer la partie nulle.

Conclusion

Comme nous l'avions montré précédemment, X₁ est une situation de jeu décidable si chacun de ces trois fils O₁,O₂ et O₃ est décidable.

Or nous venons de montrer qu'ils le sont effectivement. La situation X₁ est donc bien décidable.

De plus, parmis les différentes possibilités que nous avions énoncées sur X₁, nous sommes donc dans la configuration 2-A: aucun des trois fils O₁,O₂, O₃ n'est perdant pour les ronds et au moins un de ces trois fils mène à une partie nulle. La situation X₁ mène donc forcément à une partie nulle.

Pour terminer voici un schéma simplifié de l'arbre de jeu qui vous permettra de bien voir comment la décidabilité se propage depuis les feuilles jusqu'à la racine:

Une situation de jeu a trois valeurs possibles: Victoire, Défaite ou Nulle; selon que le joueur qui a le trait dans cette situation est respectivement certain de gagner, de perdre ou de faire partie nulle.

Les situations en vert sont celles dont la valeur est Victoire. En rouge, celles dont la valeur est Défaite. En gris, celles dont valeur est Nulle.

Si au moins un des fils d'une situation est en rouge, alors cette situation est en vert.

Si tous les fils d'une situation sont en vert ou en gris. Deux possibilités:

• Si tous les fils sont en vert (cela ne se produit pas dans l'exemple ici) alors cette situation est en rouge.
• Si au moins un fils est en gris, alors cette situation est en gris.

Preuve de la décidabilité (cas general)

La démonstration que nous allons donner ici est une preuve par récurrence. Soit S une situation de jeu, A son arbre de jeu et n la profondeur de cet arbre. Appelons J le joueur ayant le trait dans la situation S. Montrons que S est décidable quelque soit la profondeur n.

Initialisation: la propriété est évidemment vraie pour n = 0. Dans ce cas, l'arbre de jeu est réduit à un seul noeud (sa racine) et comme il s'agit également d'une feuille, il s'agit nécessairement d'une situation de fin de jeu: partie nulle ou victoire d'un des deux joueurs.

Hérédité: nous allons démontrer que si la propriété est vraie pour toute situation dont l'arbre de jeu est de profondeur inférieure ou égale à n, alors elle sera également vraie pour toute situation dont l'arbre de jeu est de profondeur inférieure ou égale à n+1.

Le schéma ci-dessous représente un arbre de jeu de profondeur n+1 et de racine S:

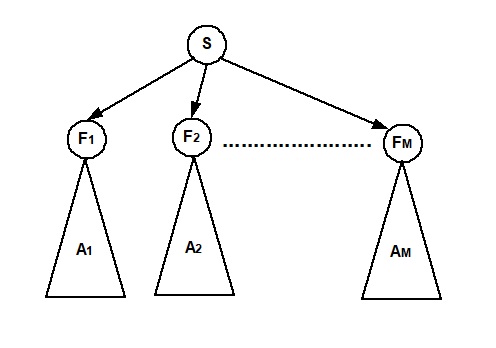
Nous pouvons supposer ici que l'arbre est de profondeur non nulle. S possède donc M fils F₁,F₂, ...,F_M où M est un entier non nul.

A₁,A₂, ...,A_M sont les arbres de jeu des situations F₁,F₂, ...,F_M. Comme l'arbre de jeu de S est de profondeur n+1, les arbres de jeu de A₁,A₂, ...,A_M sont forcément de profondeur inférieure ou égale à n. Nous pouvons donc supposer que F₁,F₂, ...,F_M sont décidables.

Il y a deux possibilités:

• Au moins une des situations F₁,F₂, ...,F_M a une valeur Défaite. Cela signifie que l'adversaire de J est certain de perdre dans cette situation. La valeur de S est donc Victoire, puisque J peut choisir le coup menant à cette situation.
• Toutes les situations F₁,F₂, ...,F_M ont une valeur Victoire ou Nulle. Dans ce cas, il y a deux possibilités:
  • Au moins une des situations F₁,F₂, ...,F_M a une valeur Nulle. La valeur de S est donc Nulle, puisque J peut choisir le coup menant à cette situation.
  • Toutes les situations F₁,F₂, ...,F_M ont une valeur Victoire. Cela signifie que l'adversaire de J gagne à tous les coups. La valeur de S est donc Defaite.

Conclusion: la situation S est bien décidable. Cela signifie que la propriété que nous avons énoncé est héréditaire et que par conséquent elle est vraie dans toutes les situations de jeu.

Conséquences pratiques

Dans les jeux pour lesquels la dimension des arbres de jeu (en terme de nombre de feuilles) reste raisonnable, il est possible de concevoir une procédure récursive capable de déterminer la valeur (Victoire, Defaite ou Nulle) d'une situation de jeu quelconque.

Le code de cette procédure (que vous serez amené à trouver par vous même en guise d'excercice) se déduit facilement de la preuve de décidabilité que nous venons de donner.

Si le jeu est bien conditionné, c'est à dire que le joueur qui commence la partie n'a pas tout de suite un coup gagnant, il est alors possible, en utilisant cette procédure, d'écrire un programme invincible.

C'est le cas en particulier du morpion. La combinatoire de ce jeu est tellement réduite, que l'arbre de jeu peut être développé entièrement par un ordinateur, même pour la situation initiale. Autrement dit, il peut précalculer toutes les parties de morpions possibles !

En jouant contre le programme Morpion-Generalise.js en version explicative, vous constaterez que si vous avez le trait dès le début, il vous indique que vous pouvez obtenir partie nulle à partir de n'importe quel coup. Ce jeu est donc bien conditionné, puisque le joueur qui commence n'a pas de coup gagnant.

Ce résultat a été obtenu en développant entièrement l'arbre de jeu du morpion à partir de la situation initiale.

Malheureusement, pour la plupart des jeux, les arbres de jeux sont généralement de dimension tellement importante, qu'il n'est pas possible de les développer entièrement en un temps raisonnable.

C'est en particulier le cas du super-morpion, ce qui explique pourquoi notre programme n'est pas invincible.

Cas particulier du jeu d'échec

Un mot sur le jeu d'échec pour terminer.

On a montré que le nombre de parties d'échecs possibles est de l'ordre de 10¹²⁰. Ce nombre énorme représente le nombre de feuilles de l'arbre de jeu de la position initiale. Il est des milliards, de milliards, de milliards, .... de fois supérieur au nombre d'atomes de l'univers. Même si l'on arrivait à développer chaque noeud de cet arbre en un milliardième de milliardième de seconde, le temps pour développer l'arbre serait encore des milliards de milliards, de milliards .... de fois supérieur à l'âge de l'univers.

D'un point de vu pratique, il est donc impossible de rendre les ordinateurs invincibles aux échecs, ni de savoir si ce jeu est bien conditionné ... (mais d'après la propriété de décidabilité cela reste néamoins théoriquement possible !!)

Il n'empêche que les ordinateurs sont actuellement très forts aux échecs. Ils l'étaient d'ailleurs déjà en 1997, l'année où Gary Kasparov, champion du monde aux échecs, a été battu par le programme Deep Blue. Je vous laisse imaginer où ils en sont aujourd'hui ...

Il est donc possible de concevoir des programmes très performants sans avoir à développer entièrement l'arbre de jeu dans chaque situation.

Mais comment ?

C'est ce que nous allons voir à présent.

Pour voir la suite du cours sur les jeux déterministe cliquez ici ou sur l'entrée Approche probabiliste du menu.